ატომისა და ელემენტარული ნაწილაკების სამყაროში გრავიტაციული ძალების უგულვებელყოფა შესაძლებელია, მათი, ნაწილაკებს შორის სხვა სახის ურთიერთქმედების ძალებთან შედარებითი, საგრძნობი სიმცირის გამო. ასევე, ჩვენ გარმომცველ სხეულებს შორისაც ძალიან რთულია გრავიტაციული ურთიერთქმედების დაკვირვება, მაშინაც კი თუ მათი მასები რამოდენიმე ათას კილოგრამს შეადგენს. მაგრამ სწორედ გრავიტაცია განსაზღვრავს ისეთი „დიდი“ ობიექტების, როგორიცაა პლანეტები, კომეტები ვარსკვლავები, ყოფაქცევას და სწორედ გრავიტაცია აკავებს ყველას და ყველაფერს დედამიწაზე.
გრავიტაცია მართავს პლანეტების მოძრაობას მზის სისტემაში. გრავიტაციის გარაშე, მზის სისტემის შემადგენელი პლანეტები სხვადასხვა მხარეს გაიქცეოდნენ და სამყაროს უკიდეგანო სივრცეში დაიკარგებოდნენ.
პლანეტების მოძრაობის კანონზომიერებები უხსოვარი დროიდან იპყრობდა ადამიანის ყურადღებას. პლანეტების მოძრაობისა და მზის სისტემის აგებულების შესწავლა გახდა გრავიტაციის თეორიის შექმნის – მსოფლიო მიზიდულობის კანონების აღმოჩენის მიზეზი.
დედამიწაზე მყოფი დამკვირვებლის თვალსაზრისით, პლანეტები საკმაოდ რთულ ტრაექტორიებზე მოძრაობენ (ნახ. 1). სამყაროს მოდელის შექმნის პირველი მცდელობა პტოლემეს ეკუთვნის (~140წ.). პტოლემემ სამყაროს ცენტრში დედამიწა მოათავსა, რომლის გარშემოც დიდ და მცირე წრეებზე პლანეტები და ვარსკვალევები მოძრაობენ.

ნახ. 1.
ვარსკვალვების ფონზე მარსის მოძრაობის პირობითი ტრაექტორია
პტოლემეს გეოცენტრულმა სისტემამ 14 ასწლელული გაძლო და მხოლოდ XVI საუკუნის შუაში იგი კოპერნიკის ჰელიოცენტრულმა სისტემამ ჩაანაცვლა. კოპერნიკის სისტემაში პლანეტების ტრაექტორიები უფრო მარტივი აღმოჩნდა.

გერმანელმა ასტრონომმა კეპლერმა XVII საუკუნის დასაწყისში კოპერნიკის სისტემის საფუძველზე მზის სისტემის პლანეტების მოძრაობის სამი ემპირიული კანონი ჩამოაყალიბა. კეპლერი დანიელი ასტრონომის ტიხო ბრაგეს პლანეტების მოძრაობაზე დაკვივებებს იყენებდა.
კეპლერის პირველი კანონი (1609 წ.):
ყოველი პლენეტის ორბიტა ელიფსია, რომლის ერთ–ერთ ფოკუსში მოთავსებულია მზე.
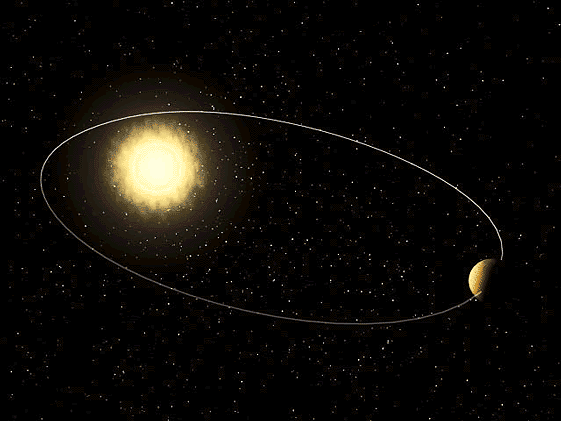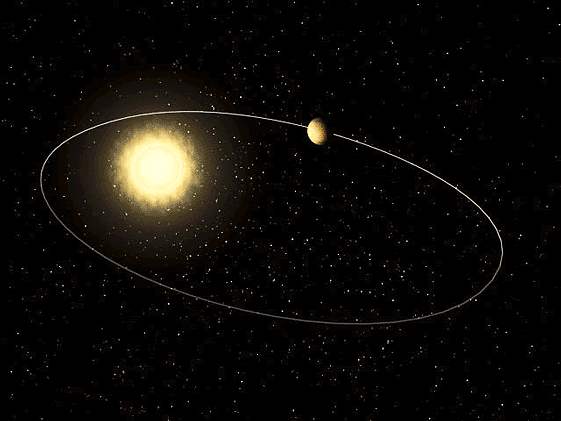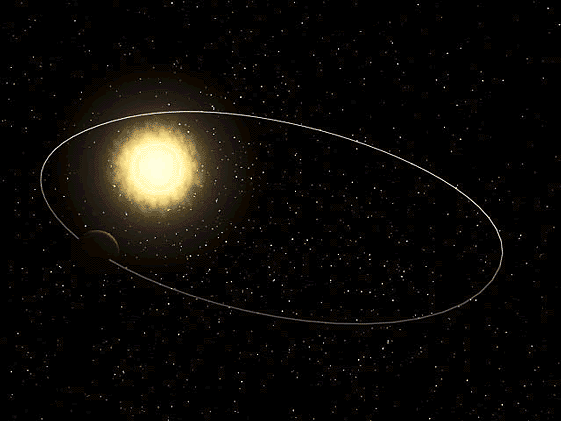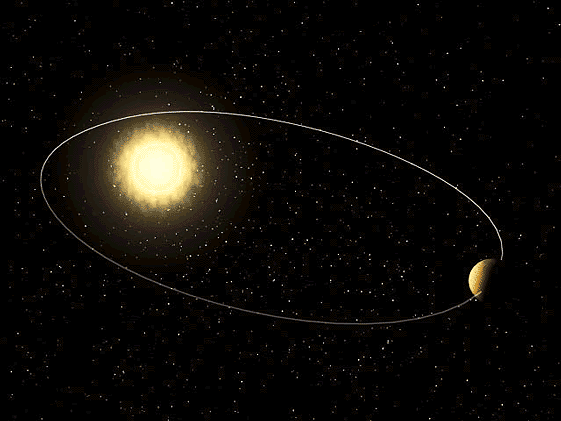
ნახ. 2–ზე მზის მასაზე გაცილების ნალკები მასის მქონე პლანეტის ელიფსური ორბიტაა ნაჩვენები. მზე ელიფსის ერთ–ერთ ფოკუსში მდებარეობს. ტრაექტორიის მზესთან უახლოესი წერტილ \(P\) –ს პერიჰელიუმი ეწოდება, მზიდან მაქსიმალურად დაშორებულ წერტილს \(A\) –ს – აფელიუმი. აფელიუმსა და პერიჰელიუმს შორის მანძილი ელიფსის დიდი ღერძია.

ნახ. 2.
\(m<<M\) მასის პლანეტის ელიფსური ორბიტა. \(a\) – დიდი ნახევარღერძის სიგრძე, \(F\) და \(F^{'}\) – ელიფსის ფოკუსები.
მზის სისტემის თითქმის ყველა პლანეტა (გარდა პლუტონისა) მოძრაობს წრეწირის მახლობელ ორბიტაზე.
კეპლერის მეორე კანონი (1609 წ.):
ყოველი პლანეტის რადიუს–ვექტორი დროის თანატოლ შუალედებში თანატოლ ფართობებს შემოწერს.

ნახ. 3 კეპლერის მეორე კანონის გრაფიკული ილუსტრაციას წარმოადგენს.
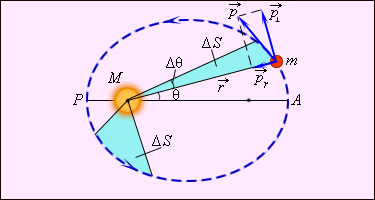
ნახ. 3.
კეპლერის მეორე კანონი – ფართობების კანონი.
კეპლერის მეორე კანონი იმპულსის მომენტების მუდმივობის კანონის ექვივალენტურია. ნახ. 3–ზე გამოსახულია სხეულის \(\vec{p}\) იმპულსი და მისი მდგენელები \(\vec{p}_{r}\) და \(\vec{p}_{\perp }\) მცირე \(\Delta t\) დროში რადიუს–ვექტორის მიერ შემოწერილი ფართობი ტოლია \(r\Delta \Theta\) ფუძისა და \(r\) სიმაღლის მქონე სამკუთხედის ფართობისა:
\(\Delta S=\frac{1}{2}r^{2}\Delta \Theta\) ან \(\frac{\Delta S}{\Delta t}=\frac{1}{2}r^{2}\frac{\Delta\Theta }{\Delta t}=\frac{1}{2}r^{2}\omega ;\: (\Delta t\rightarrow 0).\)
აქ \(\omega =\frac{\Delta \Theta }{\Delta t};\: (\Delta t\rightarrow 0)\) –კუთხური სიჩქარეა.
იმპულსის მომენტი \(L\) აბსოლუტური სიდიდით ტოლია \(\vec{p}_{\perp }\) და \(\vec{r}\) ვექტორების მოდულების ნამრავლისა:
\(L=rp_{\perp }=r(mv_{\perp })=mr^{2}\omega\) , რადგან \(v_{\perp}=r\omega.\)
ამ თანაფარდობებიდან გამოდის:
\(\frac{\Delta S}{\Delta t}=\frac{L}{2m};\: (\Delta t\rightarrow 0).\)
ამიტომ, თუ კეპლერის კანონის მიხედვით \(\frac{\Delta S}{\Delta t} =const\) , მაშინ იმპულსის მომენტი \(L\) მოძრაობისას უცვლელი რჩება.
კერძოდ, რადგან პლანეტის სიჩქარეები პერიჰელიუმში \(\vec{v}_{P}\) და აფელიუმში \(\vec{v}_{A}\) ვექტორები მიმართულია \(\vec{r}_{P}\) და \(\vec{r}_{A}\) რადიუს–ვექტორების მართობულად, იმპულსის მომენტების მუდმივობის კანონიდან გამომდინარე:
\(r_{P}v_{P}=r_{A}v_{A}.\)
კეპლერის მესამე კანონი (1619 წ.):
პლანეტების გარშემოქცევის პერიოდთა კვადრატების შეფარდება ორბიტის დიდი ნახევარღერძების კუბებთან მუდმივი სიდიდეა.
\(\frac{T^{2}}{a^{3}}=const\) ან \(\frac{T_{1}^{2}}{a_{1}^{3}}=\frac{T_{2}^{2}}{a_{2}^{3}}.\)
კეპლერის მესამე კანონი მზის სისტემის ყველა პლანეტისათვის ხორციელდება 1 %–ანი სიზუსტით.
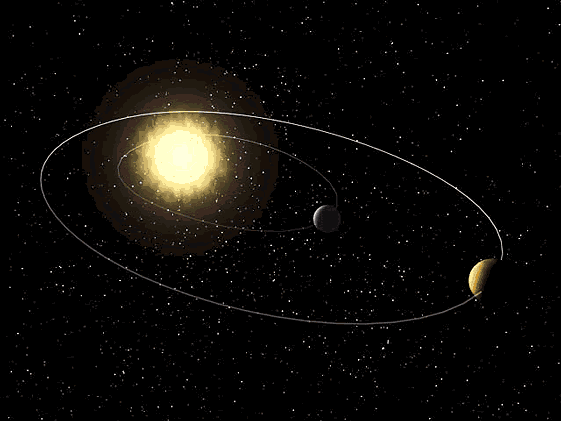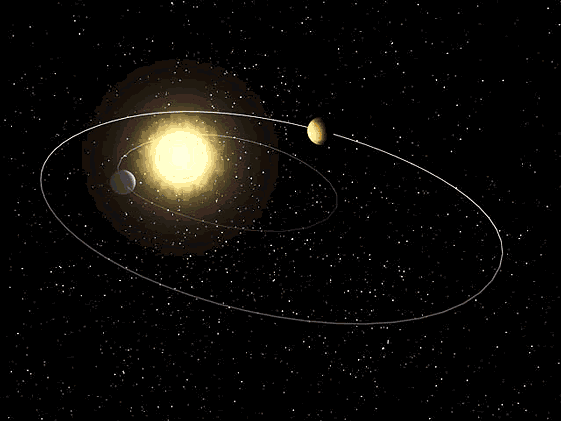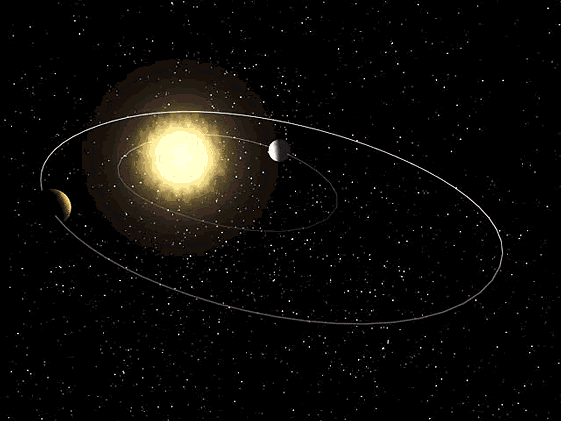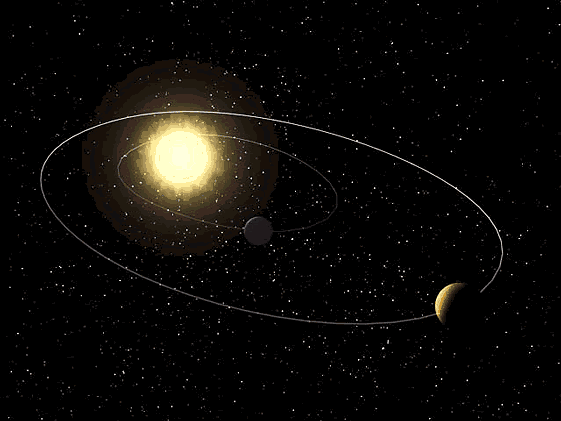
ნახ. 4–ზე გამოსახულია ორი ორბიტა, ერთ–ერთი – წრიული \(R\) რადიუსით, მეორე კი – \(a\) –ს ტოლი დიდი ნახევარღერძის მქონე ელიფსი. მესამე კანონი ამტკიცებს, რომ თუ \(R=a\) , მაშინ სხეულების გარშემოვლის პერიოდები ერთნაირია.

ნახ. 4.
წრიული და ელიფსური ორბიტები. როცა \(R=a\) , მაშინ სხეულების გარშემოვლეს პერიოდები ერთნაირია.
იმისდა მიუხედავად რომ, კეპლერის კანონები პლანეტების მოძრაობის შეცნობაში უმნიშვნელოვანეს ეტაპს წარმოადგენდა, ისინი მაინც მხოლოდ ასტრონომიული დაკვირვებებიდან მიღებულ ემპირიულ კანონებად რჩებოდა. გადამწყვეტი ნაბიჯი ამ მიმართულებით ისააკ ნიუტონმა 1682 წელს მსოფლიო მიზიდულობის კანონის აღმოჩენით გადადგა.
\(F=G\frac{Mm}{r^{2}},\)
სადაც \(M\) და \(m\) – მზისა და პლანეტის მასებია, r – მათ შორის მანძილი, G = 6,67·10–11 ნ·მ2/კგ2 – გრავიტაციული მუდმივა. ნიუტონმა პირველმა გამოთქვა მოსაზრება, რომ გრავიტაციული ძალები განსაზღვრავენ არა მხოლოდ ზმის სისტემების პლანეტების მოძრაობას; ისინი სამყაროს ნებისმიერ სხეულებს შორის მოქმედებენ. კერძოდ, ის მაშინვე ამბობდა რომ, დედამიწის ზედაპირის მახლობლად მოქმედ სიმძიმის ძალას გარავიტაციული ბუნება აქვს.
წრიული ორბიტებისათვის კეპლერის პირველი და მეორე კანონები ავტომატურად სრულდება, ხოლო მესამე კანონის მიხედვით \(T^{2}\sim R^{3}\), სადაც \(T\) – ბრუნვის პერიოდია, \(R\) – ორბიტის რადიუსი. აქედან შეიძლება გრავიტაციული ძალის მანძილზე დამოკიდებულების მიღება. წრიულ ორბიტაზე მოძრაობისას პლანეტაზე მოქმედებს ძალა, რომელიც მზესა და პლანეტას შორის გრავიტაციული ურთიერთქმედებისას აღიძვრება:
\(F\sim \omega ^{2}R=\frac{(2\pi)^{2}R}{T^{2}}.\)
თუ \(T^{2}\sim R^{3}\), მაშინ \(F\sim \frac{1}{R^{2}}.\)
გრავიტაციული ძალების კონსერვატულობის თვისება პოტენციური ენერგიის ცნების შემოტანის საშუალებას იძლევა. მსოფლიო მიზიდულობის ძალებისათვის მოხერხებულია პოტენციური ენერგიის ათვლა უსასრულოს დაშორებული წერტილიდან დაიწყოს.
გარვიტაციული ძალების მიერ \(M\) მასის უძრავი სხეულიდან \(r\) მანძილზე მდებარე \(m\) მასის სხეულის მოცემული წერტილიდან გადაადგილებისას, პოტენციური ენერგია შესრულებული მუშაობის ტოლია.
გრავიტაციულ ველში სხეულის პოტენციური ენერგიის გამოთვლის მათემატიკური პროცედურა მცირე გადაადგილებაზე შესრულებული მუშაობების აჯამვაში მდგომარეობს (ნახ. 5).

ნახ. 5.
გრავიტაციულ ველში სხეულის პოტენციური ენერგიის გამოთვლა.
მსოფლიო მიზიდულობის კანონი გამოიყენება არ მარტო წერტილოვანი მასის სხეულებისათვის, არამედ სფერულად სიმეტრიული სხეულებისათვისაც, \(\vec{F}\) გრავიტაციული ძალის \(\Delta A_{i}\) მუშაობა მცირე გადაადგილებისას \(\Delta \vec{s}_{i}=\Delta \vec{r}_{i}\) ტოლია:
\(\Delta A_{i}=-G\frac{Mm}{r_{i}^{2}}\Delta r_{i}.\)
როცა \(\Delta r_{i}\rightarrow 0\) ჯამი ინტეგრალში გადადის. გამოთვლის შედეგად პოტენციური ენერგიისათვის ვღებულობთ:
\(E_{p}=A_{r\infty }=-G\frac{Mm}{r}.\)
სადაც ნიშანი „მინუსი“ ნიშნავს, რომ გარავიტაციული ძალა მიზიდულობის ძალას წარმოადგენს.
თუ სხეული გარავიტაციულ ველში იმყოფება მიზიდულობის ცენტრიდან \(r\) მანძილზე და აქვს რაღაც \(v\) სიჩქარე, მისი სრული მექანიკური ენერგია ტოლია:
\(E=E_{k}+E_{p}=\frac{mv^{2}}{2}-G\frac{Mm}{r}=const.\)
ენერგიის მუდმივობის კანონის თანახმად სხეულის სრული მექანიკური ენერგია გრავიტაციულ ველში მუდმივი რჩება.
სრული ენერგია შეიძლება იყოს დადებითი და უარყოფითი. და ნულის ტოლიც. სრული ენერგიის ნიშანი ციური სხეულის მოძრაობის ხასიათს განსაზღვრავს (ნახ. 6).
როცა \(E=E_{1}<0\) სხეულს არ შეუძლია მიზიდელობის ცენტრიდან დაშორება \(r>r_{max}\) მანძილზე. ასეთ შემთხვევაში ციური სხეული ელიფსურ ორბიტაზე მოძრაობს (მზის სისტემის პლანეტები, კომეტები).

ნახ. 6.
\(m\) მასის სხეულის ენერგიის დიაგრამა, სფერული სიმეტრიის მქონე \(M\) მასისა და \(R\) რადიუსის სხეულის მიერ შექმნილ, გრავიტაციულ ველში.
როცა \(E=E_{2}=0\) სხეულს შეუძლია უასარულოდ დაშორება. სხეულის სიჩქარე უსასრულიბაში ნულის ტოლი იქნება. სხეული პარაბოლურ ტრაექტორიაზე მოძრაობს. როცა \(E=E_{3}>0\) მოძრაობა ჰიპერბოლურ ტრაექტორიაზე ხდება. სხეული უსასრულობისკენ მიემართება ენერგიის მარაგით.
კეპლრის კანონები გამოიყენება არა მხოლოს მზის სისტემის პლანეტებისა და სხვა სხეულების მოძრაობისათვის, არამეს დედამიწის ხელოვნული თანამგზავრებისა და კოსმოსური ხომალდების მოძრაობისათვისაც.
პირველ კოსმოსურ სიჩქარეს უწოდებენ თანამგზავრის მოძრაობის სიჩქარეს, რომელიც დედამიწის მახლობელ წრიულ ორბიტაზე მოძრაობს.
\(\frac{mv_{1}^{2}}{R_{3}}=G\frac{Mm}{R_{3}^{2}}=gm,\)
აქედან:
\(v_{1}=\sqrt{G\frac{M}{R_{3}}}=\sqrt{gR_{3}}=7,9\cdot 10^{3}\) მ/წმ.
მეორე კოსმოსურ სიჩქარეს უწოდებენ მინიმალურ სიჩქარეს, რომელიც უნდა მიანიჭონ კოსმოსურ ხომალდს დედამიწის ზედაპირთან, რომ მან გადალახოს დედამიწის მიზიდულობა, გადაიქცეს მზის ხელოვნურ თანამგზავრად (ხელოვნურ პლანეტად). ამასთან ხომალდი დედამიწას სცილდება პარაბოლური ტრაექტორიით.
\(E=\frac{mv_{2}^{2}}{2}-G\frac{Mm}{R_{3}}=0,\)
აქადან:
\(v_{2}=\sqrt{2G\frac{M}{R_{3}}}=\sqrt{2gR_{3}}=11,2\cdot 10^{3}\) მ/წმ.
ნახ. 7–ზე კოსმოსური სიჩქარეების ილუსტრაციაა მოცემული, თუ კოსმოსური ხომალდის სიჩქარე \(v_{1}=7,9\cdot 10^{3}\) მ/წმ–ს ტოლია და მიმართულება დედამიწის ზედაპირის პარალელურია, მაშინ ხომალდი დედამიწის ზედაპირიდან მცირე სიმაღლეზე წრიულ ორბიტაზე იმოძრავებს. როცა საწყისი სიჩქარე \(v_{1}\)–ს აღემატება, მაგრამ ნაკლებია \(v_{2}=11,2\cdot 10^{3}\) მ/წმ–ზე, ხომალდის ორბიტა ელიფსურია. \(v_{2}\)–ის ტოლი საწყისი სიჩქარის დროს ხომალდი პარაბოლაზე მოძრაობს, უფრო დიდ სიჩქარეებზე კი – ჰიპერბოლაზე.

ნახ. 7.
კოსმოსური სიჩქარეები.მითითებულიადედამიწის ზედაპირის მახლობელი სიჩქარეები. 1: \(v=v_{1}\) – წრიული ტრაექტორია; 2: \(v_{1}<v<v_{2}\) – ელიფსური ტრაექტორია; 3:\(v=11,1\cdot 10^{3}\) м/с – ძლიერად გაჭიმული ელიფსი; 4: \(v=v_{2}\) – პარაბოლურიტრაექტორია 5: \(v>v_{2}\) – ჰიპერბოლური ტრაექტორია; 6: მთვარის ტრაექტორია.