გადატანითი და ბრუნვითი მოძრაობების გვერდით მექანიკაში მნიშვნელოვანი ადგილი რხევით მოძრაობას უკავია. მექანიკურ რხევებს უწოდებენ სხეულის რხევებს, რომლებიც ზუსტად (ან დაახლოებით) მეორდება ერთნაირი დროის ინტერვალებში. მოძრავი სხეულის მოძრაობას კანონი დროის რაღაც პერიოდული \(x=f(t)\) ფუნქციაა. ამ ფუნქციის გრაფიკული გამოსახულება რხევითი პროცესის დროში მიმდინარეობაზე ნათელ წარმოდგენას იძლევა.
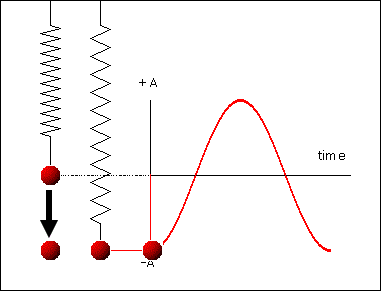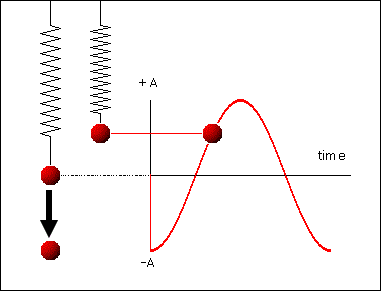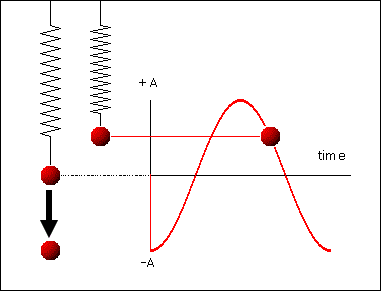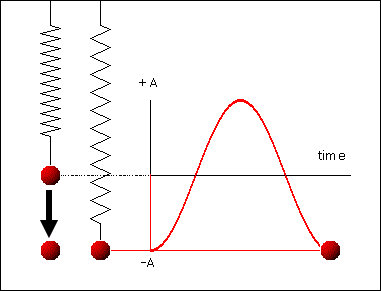
რხევითი სისტემების უბრალო მაგალითს ზამბარაზე დაკიდებული ტვირთი ან მათემატიკური ქანქარა წარმოადგენს (ნახ. 1).
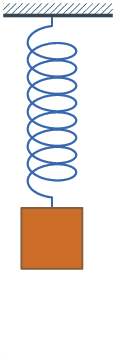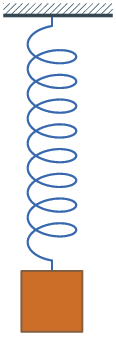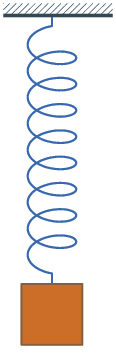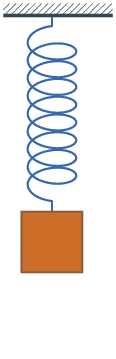

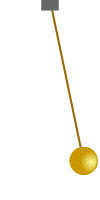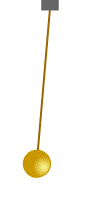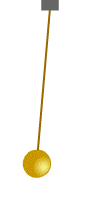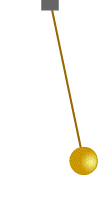
ნახ.1
მექანიკური რხევითი სისტემა
მექანიკური რხევები, ისევე როგორც ნებისმიერი ბუნების რხევითი პროცესები, შიძლება იყოს თავისუფალი და იძულებითი. თავისუფალი რხევა, მას შემდეგ რაც სისტემა გამოყვანილ იქნა წონასწორობის მდგომარეობიდან, სრულდება სისტემის შიგა ძალების მოქმედებით. ზამბარაზე დაკიდებული ტვირთის რხევა ან მათემატიკური ქანქარას რხევა თავისუფალ რხევას წარმოადგენს. რხევას, რომელიც გარე, პერიოდულად ცვლადი ძალიების მოქმედებით ხდება, იძულებითი ეწოდება
რხევითი პროცესის უმარტივეს სახეს ჰარმონიული რხევები წარმოადგენენ, რომლებიც შემდეგი განტოლებით აღიწერება:
\(x=x_{m}\cos (\omega t+\phi _{0})\).
აქ \(x\) – წონასწორობის მდგომარეობიდან გადახრაა, \(x_{m}\) – რხევის ამპლიტუდაა, ე.ი. წონასწორობიდან მაქსიმალური გადახრა, \(\omega\) – რხევის ციკლური ან წრიული სიხშირე, \(t\) – დრო. კოსინუსის ქვეშ მყოფ სიდიდეს \(\phi=\omega t+\phi _{0}\) ჰარმონიული პროცესისფაზას უწოდებენ. როცა \(t=0\), \(\phi=\phi_{0}\), ამიტომ \(\phi_{0}\) საწყის ფაზას უწოდებენ. დროის მინიმალირი ინტერვალი, რომლის შემდეგაც სხეულის მოძრაობა მეორდება რხევის პერიოდს \(T\) უწოდებენ. რხევის პერიოდის შებრუნებულ ფიზიკურ სიდიდეს რხევის სიხშირეს უწოდებენ:
\(f=\frac{1}{T}.\)
რხევის \(f\) სიხშირე აჩვენებს, რამდები რხევა შესრულდა 1 წამში. სიხშირის ერთეილია – ჰერცი. რხევის \(f\) სიხშირე დაკავშირებულია ციკლურ სიხშირესთან და რხევის პერიოდთან შემდეგი თანაფარდობით:
\(\omega=2\pi f=\frac{2\pi}{T}.\)
ნახ. 2–ზე გამოსახულია ჰარმონიული რხევის დროს, სხეულის მდებარეობები დროის ტოლ მონაკვეთებში. ასეთი სურათის მიღება შესაძლებელია ექსპერიმენტულად მერხევი სხეულის სინათლით მოკლე პერიოდული პორციებით განათებისას (სტრობოსკოპული განათება). ისრები სხეულის სიჩქარის ვექტორებს გამოსახავს დროის სხვადასხვა მომენტში.

ნახ. 2.
ჰარმონიული რხევის სტრობოსკოპული გამოსახულება. საწყისი ფაზა \(\phi_{0}=0\). სხეულის თანმიმდევრულ მდებარეობებს შორის დროის ინტერვალი \(\tau =\frac{T}{12}.\)
ნახ. 3–ზე ნაჩვენებია ცვლილებები, რომლებიც ხდება ჰარმონიული პროცესის გრაფიკზე, თუ იცვლება რხევის ამპლიტუდა \(x_{m}\), პერიოდი \(T\) (ან სიხშირე \(f\) ), ან საწყისი ფაზა \(\phi_0\).
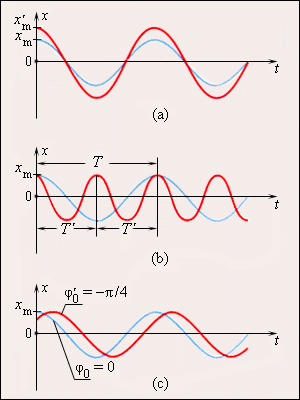
ნახ. 3.
ყველა შემთხვევაში ლურჯი მრუდისთვის \(\phi_{0}=0\): \(a\) – წითელი მრუდი ლურჯისგან განსხვავდება მხოლოდ დიდი ამპლიტუდით (\(x_{m}^{'}>x_{m}\)); \(b\) – წითელი მრუდი ლურჯისგან განსხვავდება მხოლოდ პერიოდის მნიშვნელობით (\(T^{'}=\frac{T}{2}\)); \(c\) – წითელი მრუდი ლურჯისგან განსხვავდება მხოლოდ საწყისი ფაზის მნიშვნელობით (\(\phi_0^{'}=-\frac{\pi}{2}\) რად).
წრფის გასწვრის სხეულის (\(OX\) ღერძი) რხევითი მოძრაობის დროს სიჩქარის ვექტორი ყოველთვის მიმართულია ამ წრფის გასწვრივ.სხეულის სიჩქარე \(v=v_{x}\) განისაზღვრება გამოსახულებით
\(v=\frac{\Delta x}{\Delta t};\: \: (\Delta t\rightarrow 0).\)
როცა \(\Delta t\rightarrow 0\) , \(\frac{\Delta x}{\Delta t}\) ფარდობის ზღვრის პოვნის მათემატიკურ პროცედურას \(x(t)\) ფუნქციისათვის \(t\) დროით წარმოებულის გამოთვლას უწოდებენ და აღნიშნავენ \(\frac{dx(t)}{dt}\) –ით ან \({x}'(t)\) –ით. მოძრაობის ჰარმონიული კანონისათვის \(x=x_{m}\cos (\omega t+\phi_{0})\) წარმოებულის გამოთვლას შემდეგ შედეგებამდე მივყავართ:
\(v={x}'(t)=-\omega x_{m}\sin (\omega t+\phi_{0})=\omega x_{m}\cos \left ( \omega t+\phi_{0}+\frac{\pi}{2} \right ).\)
კოსინუსის არგუმენტში \(+\frac{\pi}{2}\) შესაკრების გამოჩენა საწყისი ფაზის ცვლილებას აღნიშნავს. სიჩქარის მოდულით მაქსიმალური მნიშვნელობები \(v=\omega x_{m}\) დროის იმ მომენტებში მიიღწევა, როცა სხეული წონასწორობის მდებარეობებს გადის (\(x=0\)). ანალოგიურად განისაზღვრება ჰარმონიული რხევისას სხეულის აჩქარებაც \(a=a_{x}\):
\(a=\frac{\Delta v}{\Delta t};\: \: (\Delta t\rightarrow 0),\)
აქდან გამომდინარე, აჩქარება \(a\) ტოლია \(v(t)\) ფუნქციის წარმოებულისა \(t\) დროით, ან \(x(t)\) ფუნქციის მეორე წარმოებულის. გამოთვლების შედეგად ვღებულობთ:
\(a={v}'(t)={x}''(t)=-\omega^{2}x_{m}\cos (\omega t+\phi_{0})=-\omega^{2}x(t).\)
ამ გამოსახულებაში ნიშანი მინუსი აღნიშნავს, რომ \(a(t)\) აჩქარებას ყოველთვის \(x(t)\) გადაადგილების საწინააღმდეგო ნიშანი აქვს და, ე.ი. ნიუტონის მეორე კანონის თანახმად ჰარმონიული რხევის გამომწვევი ძალა ყოველთვის მიმართულია წონასწორობის მდებარეობისაკენ (\(x=0\) ).
ნახ. 4–ზე მოყვანილია ჰარმონიული რხევისას სხეულის კოორდინატის, სიჩქარისა და აჩქარების გრაფიკები.
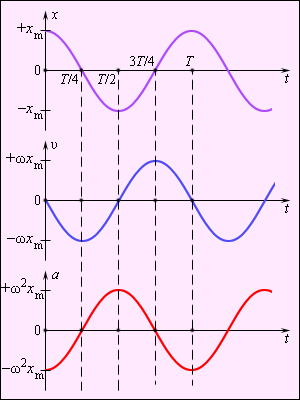
ნახ. 4.
ჰარმონიულად მერხევი სხეულის კოორდინატის \(x(t)\), სიჩქარის \(v(t)\) და აჩქარების \(a(t)\) გრაფიკები.