სხვადასხვა კონფიგურაციის მუდმივი დენის მაგნიტული ველები ექსპერიმენტულად ფრანგმა მეცნიერებმა ჟ.ბიომ და ფ.სავარმა ()1820 წ.) შეისწავლეს. ისინი მივიდნენ დასკვნამდე, რომ სადენებში გამავალი დენების მაგნიტური ველის ინდუქცია განისაზღვრება გამტარების ყველა ცალკეული უბნის საერთო მოქმედებით. მაგნიტური ველი სუპერპოზიციის პრინციპს ექვემდებარება:
თუ მაგნიტური ველი რამოდენიმე დენიანი სადენისგანაა შექმნილი, ტოლქმედი ველის ინდუქცია ცალცალკეული გამტარის მიერ შექმნილი ველების ინდუქციების ჯამის ტოლია.
დენიანი გამტარის \(\vec{B}\) ინდუქცია შეიძლება წარმოდეგნილი იქნეს გამტარის ცალცალკეული უბნების მიერ შექმნილი ელემენტარული \(\Delta \vec{B}\) ინდუქციების ვექტორული ჯამის სახით. ცდისას შეუძლებელია დენიანი გამტარის ცალკეული უბნების გამოყოფა, რადგან მუდმივი დენი ყოველთვის ჩაკეტილია. შეიძლება გაიზომოს მხოლოდ ჯამური ინდუქცია მაგნიტური ველისა, რომელსაც დენის ყველა ელემენტი ქმნის. ბიო-სავარის კანონი განსაზღვრავს I სიგრძის დენიანი გამტარის მცირე Δl სიგრძის უბნის მიერ შექმნილ მაგნიტურ \(\Delta \vec{B}\) ინდუქციის წვლილს ჯამური მაგნიტური ველის \(\vec{B}\) ინდუქციაში.
\(\Delta \vec{B}=\frac{\mu _{0}I\Delta l\sin \alpha }{4\pi r^{2}}\)
აქ r – მოცემული Δl უბნიდან დაკვირვების წერტილამდე მანძილია, α –დაკვირვების წერტილისკენ მიმართულებასა და მოცემულ უბანში დენის მიმართულებას შორი კუთხეა, μ0 – მაგნიტური მუდმივაა. \(\Delta \vec{B}\) ვექტორის მიმართულება ბურღის წესით განისაზღვრება: იგი ემთხვევა ბურღის სახელურის ბრუნვის მიმართულებას , როცა ბურღვის მიმართულება ემთხვევა დენის მიმართულებას. ნახ. 1 იძლევა ბიო-სავარის კანონის ილუსტრაციას წრფივი დენიანი გამტარის მაგნიტური ველის მაგალითზე. თუ მაგნიტურ ველში წრფივი დენიანი გამტარის ყველა ცალკეული უბნის წვლილის აჯამვას (ინტეგრირებას) მოვახდენთ, წრფივი დენის მაგნიტური ინდუქციისთვის მივიღებთ ფორმულას:
\(B=\frac{\mu _{0}}{2\pi }\frac{I}{R}\).
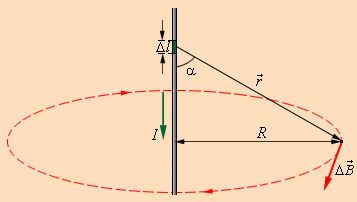
ნახ. 1.
ბიო-სავარას კანონის ილუსტრაცია
ბიო-სავარის კანონი სხვადსხვა კონფიგურაციის დენების მაგნიტური ველების გათვლის საშუალებას იძლევა. მაგალითად, ძნელი არ არის წრიული დენის ცენტრში მაგნირური ველის გამოთვლა. ამ გამოთვლებს მივყავართ ფორმულამდე
\(B=\frac{\mu _{0}}{2 }\frac{I}{R}\)
სადაც R – წრიული გამტარის რადიუსია. \(\vec{B}\) ვექტორის მიმართულების განსაზღვრისთვის ბურღის წესის გამოყენებაა შესაძლებელი, ოღონდ ახლა სახელური უნდა ვაბრუნოთ წრიული დენის მიმართულებით, ხოლო ბურღვის მიმართულება მაგნიტური ველის ინდუქციის ვექტორის მიმართულებას ემთხვევა.
მაგნიტური ველის გათვლები ხშირად მაგნიტური ველის შემქმნელი დენის კონფიგურაციის სიმეტრიის გათვალისწინებით მარტივდება. ამ შემთხვევაში შეიძლება მაგნიტური ინდუქციის ვექტორის ცირკულაციის თეორიის გამოყენება, რომელიც დენების მაგნიტური ველის თეორიაში იგივე როლს ასრულებს, რასაც გაუსის თეორემა ელექტროსტატიკაში.
ავხსნათ \(\vec{B}\) ვექტორის ცირკულაციის ცნება. ვთქვათ სივრცეში, სადაც მაგნიტური ველია შექმნილი, არჩეულია რაღაც პირობითი ჩაკეტილი კონტური (არა აუცილებლად ბრტყელი) და მითითებულია მისი შემოვლის დადებითი მიმართულება. ყოველ ცალკეულ მცირე Δl უბანზე შეიძლება განისაზრვროს მოცემული უბნის \(\vec{B}\) ვექტორის მხებზე \(B_{l}\) მდგენელი, ე.ი. განისაზღვროს კონტურის მოცემულ უბანში მხების მიმართულებაზე \(\vec{B}\) ვექტორის პროექცია (ნახ. 2).

ნახ. 2.
წინასწარ მითითებული შემოვლის მიმართულების მქონე ჩაკეტილი (L) კონტური. გამოსახულია მაგნიტური ველის წარმომქმნელი I1, I2 და I3 დენები
\(\vec{B}\) ვექტორის ცირკულაციას უწოდებენ მთელ L კონტურზე აღებული \(B_{l}\Delta l\) ნამრავლების ჯამს:
ცირკულაცია ვექტორისა \(\vec{B}=\sum_{\left ( L \right )}B_{l}\Delta l\)
მაგნიტური ველის შემქმნელი ზოგი დენი შეიძლება მსჭვალავდეს L კონტურს, მაშინ როცა სხვები კონტურს მიღმა რჩებოდნენ.
ცირკულაციის თეორამა ამტკიცებს, რომ მუდმივი დენების მაგნიტური ველის \(\vec{B}\) ვექტორის ნებისმიერ L კონტურზე ცირკულაცია ყოველთვის მაგნიტური მუდმივის კონტურის განმსჭვალავ ყველა დენის ჯამზე ნამრავლის ტოლია:
\(\sum_{\left ( L \right )}B_{l}\Delta l=\mu _{0}\sum I_{i}\)
მაგალითის სახით ნახ. 2-ზე რამდენიმე მაგნიტური ველის შემქმნელი დენიანი გამტარია გამოსახული. I2 და I3 დენები L კონტურს მსჭვალავენ ურთიერთსაწინააღმდეგო მიმართულებით. მათ სხვდასხვა ნიშანი უნდა მიეწეროს - დადებითად უნდა ჩაითვალის დენები, რომლებიც კუნტურის შემოვლის მარჯვენა ბურღის წესთან არიან დაკავშირებული. ესე იგი , I3 > 0, ხოლო I2 < 0. I1 დენი კონტურს არ მსჭვალავს.
ამ მაგალითისთვის ცირკულაციის თეორემას აქვს სახე:
\(\sum_{\left ( L \right )}B_{l}\Delta l=\mu _{0}\left ( I_{3}-I_{2} \right )\)
ზოგადი სახით ცირკულაციის თეორემა ბიო-სავარას კანონიდან და სუპერპუზიციის პრინციპიდან გამოდის.
ცირკულაციის თეორემის გამოყენების უბრალო მაგალითს წარმოსდგენს წრფივი დენიანი გამტარის ველის მაგნიტური ინდუქციის ფორმულის გამოყვანა. მოცემული ამოცანის სიმეტრიის გათვალიწინებით, მიზანშეწონილია R რადიუსიანი წრიული L კონტურის არჩევა, რომელიც გამტარის მართობულ სიბრტყეში მდებარეობს. სიმეტრიიდან გამომდინარე \(\vec{B}\) ვექტორი მიმართულია \(\left (B_{l}=B \right )\) მხების გასწვრივ, ხოლო მისი სიდიდე ერთნაირია წრეწირის ყველა წერტილში. ცირულაციის თეორემის გამოყენება იძლევა ტოლობას:
\(\sum_{\left ( L \right )}B_{l}\Delta l=2\pi RB=\mu _{0}I\)
აქედან გამოდის ადრე მოყვანილი წრფივი დენიანი გამტარის ველის მაგნიტური ინდუქციის სიდიდის ფორმულა.
ეს მაგალით უჩვენებს, რომ თეორემა მაგნიტური ველი \(\vec{B}\) ინდუქციის ცირკულაციის შესახებ შეიძლება გამოყენებული იქნეს ისეთი მაგნიტური ველების გათვლისთვის, რომლებიც დენების სიმეტრიული განაწილებით იქმნება, როცა სიმეტრიის მოსაზრებებიდან გამომდინარე შეიძლება „გამოვიცნოთ“ ველის საერთო სრუქტურა.
პრაქტიკაში არსებობს ცირკულაციის თეორიით მაგნიტური ველების გათვლის არა ერთი მაგალითი. ერთი ასეთი მაგალითია ტოროიდული კოჭას ველის გამოთვლის ამოცანა. (ნახ. 3).
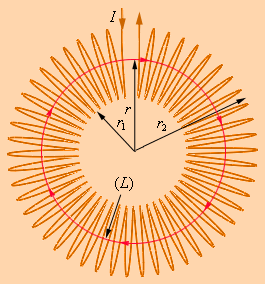
ნახ. 3.
ტოროიდულ კოჭასათვის ცირკულაციის თეორემის გამოყენების მაგალით
იგულისხმება, რომ კოჭა მჭიდროდ. ე.ი. ხვიახვიაზეა დახვეული არამაგნიტურ ტოროიდულ გულზე. ასეთ კოჭაში მაგნიტური ინდუქციის წირები კუჭას შიგნით არიან ჩაკეტილი და კონცენტრულ წრეწირებს წარმოადგენენ. ისინი ისე არიან მიმართული, რომ მათ გასწვრივ ყურების შემთხვევაში, ჩვენ ხვეულებში უნდა დავინახოთ დენი, რომელიც საათის ისრის მიმართულების ცირკულირებს. იგი ნახ. 3-ზე გამოსახულია ერთერთი r1 ≤ r < r2 რადიუსიანი წირის სახით. მივუყენოთ ცირკულაციის თეორემა L წრიულ კონტურს, რომელიც ნახ. 3-ზე გამოსახულ მაგნიტული ველის ინდუქციის წირს ემთხვევა. სიმეტრიის მოსაზრებებიდან გამომდინარე ნათელია, რომ \(\vec{B}\) ვექტორის სიდიდე მთელი ამ წირის გასწვრივ ერთნაერია. ცირკულაციის თეორემის მიხედვით შეიძლება ჩავწეროთ:
B ∙ 2πr = μ0IN,
სადაც N – ხვეულების სრული რიცხვი, ხოლო I – კოჭას ხვეულებში გამავალი დენია. აქედან გამომდინარე,
\(B=\frac{\mu \mu _{0}IN}{2\pi r}\)
ამგვარად, მაგნიტური ინდუქციის ვექტორის სიდიდე ტოროიდულ კოჭაში r რადიუსზეა დამოკიდებული. თუ კოჭას გული თხელია, ე.ი. r2 – r1 << r, მაშინ კოჭას შიგნით მაგნიტური ველი პრაქტიკულად ერთგვაროვანია. სიდიდე n = N / 2πr კოჭას სირძის ერთეულძე ხვიათა რიცხვს წარმოადგენს. ასეთ შმთხვევაში
B = μ 0I n.
ამ გამოსახულებაში ტორის რადიუსი არ შედის, ამიტომ იგი ზღვრულ r → ∞ შემთხვევაშიც სამართლიანია. მაგრამ ზღვარში ტოროიდული კოჭას ყოველი ნაწილი შეიძლება განვიხილოთ, როგორც გრძელი წრფივი კოჭა. ასეთ კოჭებს სოლეიდონებს უწოდებენ. სოლეიდონის ბოლოებიდან დაშორებით მაგნიტური ინდუქციის სიდიდე ტოროიდული კოჭას მსგავსი ფორმულით გამოისახება.
ნახ. 4-ზე სასრული სიგრძის კოჭას მაგნიტური ველია გამოსახილი. ყურადღება უნდა მიექცეს იმას, რომ კოჭას ცენტრალურ ნაწილში მაგნიტური ველი პრაქტიკულად ერთგვაოვანია და გაცილებით ძლიერია ვიდრე კოჭას გარეთ. ამაზე მაგნიტული ინდუქციის წირების სიხშირე მიუთითებს. უსასრულოდ გრძელი სოლეიდონის ზღვრულ შემთხვევაში ერთგვაროვანი მაგნიტური ველი მთლიანად მასშია თავმოყრილი.
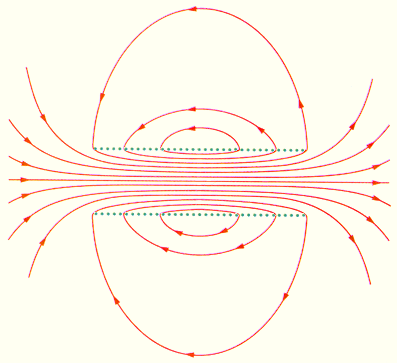
ნახ. 4.
სასრული სიგრძის კოჭას მაგნიტური ველი. სოლეიდონის ცენტრში მაგნიტური ველი პრაქტიკულად ერთგვაროვანია და სიდიდი მნიშვნელოვნად აჭარბებს კოჭას გარე ველს
უსასრულიდ გრძელი სოლეიდონის შემთხვევაში გამოსახულება მაგნიტური ველის ინდექციისთვის შეიძლება მივიღოთ უშუალოდ ნახ. 5-ზე ნაჩვენები მართხკუთხა კონტურისათვის ცირკულაციის თეორემის გამოყენებით.

ნახ. 5.
ცირკულაციის თეორიის გამოყენება უსასრულოდ გრძელი სოლეიდონის მაგნიტური გათვლისთვის
მაგნიტური ინდუქციის ვექტორს ნულისაგან განსხვავებული გეგმილი აქვს abcd კონტურის მხოლოდ ab გვერდზე. აქედან გამომდინარე, \(\vec{B}\) ვექტორის კონტურის ირგვლივ ცირკულაცია \(Bl\) -ის ტოლია, სადაც \(l\) - ab გვერდის სიგრძეა. სოლეინოიდის ხვიათა რიცხვი, რომლებიც abcd კონტურს მსჭვალევენ, ტოლია \(n-l\), სადაც n – სოლეიდონის სიგრძის ერთეულზე ხვიათა რიცხვია, ხოლო კონტურის გამსჭვალევი სრული დენი ტოლია \(Inl\) . ცირკულაციის თეორიის თანახმად,
\(Bl=\mu _{0}Inl\),
აქედან
\(B=\mu _{0}In\)
ეს გამოსახულება ადრე მიღებულ თხელი ტოროიდული კოჭას მაგნიტური ველის ფორმულას ემთხვევა.